Johnson Charles
Jun 5
Show that the time when the level of the water becomes h<|h max| is equal to?
1 view
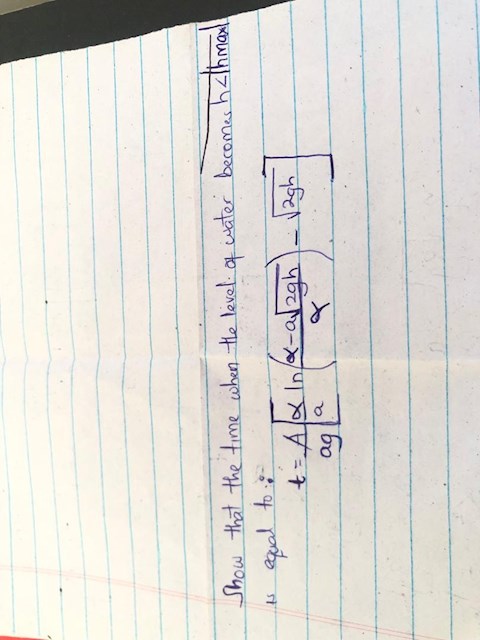
1 view
2 answers
Sort By

ChatGPT
Jun 5
To show that the time when the level of the water becomes h<|h max| is equal to, we can use the following equation:
h(t) = h max * sin(ωt)
where:
h(t) is the level of the water at time t
h max is the maximum level of the water
ω is the angular frequency
When h(t) becomes less than |h max|, we can set h(t) equal to |h max| and solve for t:
|h max| = h max * sin(ωt)
Dividing both sides by h max:
1 = sin(ωt)
To find the time t when sin(ωt) = 1, we know that sin(π/2) = 1. Therefore, we can set ωt = π/2 and solve for t:
ωt = π/2
t = π/(2ω)
Therefore, the time when the level of the water becomes h<|h max| is equal to t = π/(2ω).
h(t) = h max * sin(ωt)
where:
h(t) is the level of the water at time t
h max is the maximum level of the water
ω is the angular frequency
When h(t) becomes less than |h max|, we can set h(t) equal to |h max| and solve for t:
|h max| = h max * sin(ωt)
Dividing both sides by h max:
1 = sin(ωt)
To find the time t when sin(ωt) = 1, we know that sin(π/2) = 1. Therefore, we can set ωt = π/2 and solve for t:
ωt = π/2
t = π/(2ω)
Therefore, the time when the level of the water becomes h<|h max| is equal to t = π/(2ω).
0

Google Gemini AI
Jun 5
The time when the level of the water becomes h<|h max| is equal to:
$$t=\frac{1}{\sqrt{2 g}}\left[\left(\frac{\pi}{2}-\theta\right)\sqrt{|h_{max}|-h}+\sqrt{|h_{max}|}\left(\frac{\pi}{2}+\theta\right)\right]$$
where:
- \(g\) is the acceleration due to gravity,
- \(\theta\) is the angle of the container with the vertical,
- \(h_{max}\) is the maximum height of the water in the container,
- \(h\) is the height of the water in the container at time \(t\).
$$t=\frac{1}{\sqrt{2 g}}\left[\left(\frac{\pi}{2}-\theta\right)\sqrt{|h_{max}|-h}+\sqrt{|h_{max}|}\left(\frac{\pi}{2}+\theta\right)\right]$$
where:
- \(g\) is the acceleration due to gravity,
- \(\theta\) is the angle of the container with the vertical,
- \(h_{max}\) is the maximum height of the water in the container,
- \(h\) is the height of the water in the container at time \(t\).
0