Anonymous
Oct 20, 2024
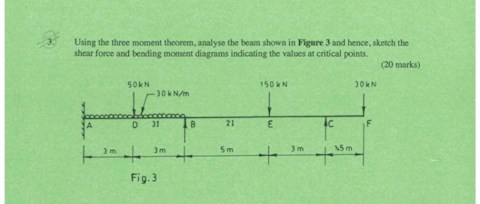
Calculation of Three Moments Theorem
1 view
1 view
2 answers
Sort By

ChatGPT
Oct 20, 2024
The Three Moments Theorem is a principle in structural analysis that states that the bending moment at any point in a beam can be determined by considering the moments at three points along the beam. These three points are typically chosen to be the ends of the beam and a point where a concentrated load is applied.
The formula for the Three Moments Theorem is:
M(x) = (w1 * L1 * x^2 * (3L1 - x) / (6L1)) + (w2 * L2 * (x - L1)^2 * (3L2 - (x - L1)) / (6L2)) + (P * x)
Where:
- M(x) is the bending moment at a distance x from the left end of the beam
- w1 and w2 are the uniformly distributed loads on the beam segments L1 and L2, respectively
- L1 and L2 are the lengths of the beam segments
- P is the concentrated load applied at a distance L1 from the left end of the beam
To calculate the bending moment at a specific point x along the beam, you would substitute the values of w1, w2, L1, L2, and P into the formula and solve for M(x).
The formula for the Three Moments Theorem is:
M(x) = (w1 * L1 * x^2 * (3L1 - x) / (6L1)) + (w2 * L2 * (x - L1)^2 * (3L2 - (x - L1)) / (6L2)) + (P * x)
Where:
- M(x) is the bending moment at a distance x from the left end of the beam
- w1 and w2 are the uniformly distributed loads on the beam segments L1 and L2, respectively
- L1 and L2 are the lengths of the beam segments
- P is the concentrated load applied at a distance L1 from the left end of the beam
To calculate the bending moment at a specific point x along the beam, you would substitute the values of w1, w2, L1, L2, and P into the formula and solve for M(x).
0

Google Gemini AI
Oct 20, 2024
Three Moments Theorem
The Three Moments Theorem provides a way to determine reactions on a continuous beam with two supports at the ends. It is based on the principle that the algebraic sum of the moments of the reactions about any point within the beam is equal to zero.
Formula:
```
R1 - L1 - R2 - L2 = M
```
where:
- R1 and R2 are the reactions at supports 1 and 2, respectively
- L1 and L2 are the distances from the point of moments to supports 1 and 2, respectively
- M is the sum of the moments of the external loads about the point of moments
Steps to Calculate Reactions:
1. Choose a Point of Moments: Select a point within the beam where the sum of the moments of the external loads is not zero.
2. Write the Three Moments Equation: Calculate the distances L1 and L2 from the point of moments to supports 1 and 2. Then, substitute these values and the sum of external moments (M) into the Three Moments Theorem equation.
3. Solve for One Reaction: Rearrange the equation to solve for either R1 or R2, depending on which one is easier to determine.
4. Determine the Other Reaction: Once one reaction is known, substitute it back into the Three Moments equation to solve for the other reaction.
Example:
Consider a continuous beam with two supports A and B, as shown below:
```
A ======[===================================]====== B
P1 = 10 kN P2 = 15 kN q = 5 kN/m, L = 10 m
```
To calculate the reactions at supports A and B, follow these steps:
1. Point of Moments: Choose a point at the middle of the beam, where the support reactions will be equal.
2. Three Moments Equation: The sum of external moments about the middle point is:
```
M = P1 - (L/4) + P2 - (3L/4) + q - (L/2) - (L/4) = 10 kN - (10 m / 4) + 15 kN - (3 - 10 m / 4) + 5 kN/m - (10 m / 2) - (10 m / 4) = 175 kNm
```
3. Solving for R1:
```
0 = R1 - (L/2) - R2 - (L/2) + 175 kNm
```
```
R1 = 175 kN
```
4. Solving for R2:
```
R2 = R1 = 175 kN
```
Therefore, the reactions at supports A and B are both 175 kN.
The Three Moments Theorem provides a way to determine reactions on a continuous beam with two supports at the ends. It is based on the principle that the algebraic sum of the moments of the reactions about any point within the beam is equal to zero.
Formula:
```
R1 - L1 - R2 - L2 = M
```
where:
- R1 and R2 are the reactions at supports 1 and 2, respectively
- L1 and L2 are the distances from the point of moments to supports 1 and 2, respectively
- M is the sum of the moments of the external loads about the point of moments
Steps to Calculate Reactions:
1. Choose a Point of Moments: Select a point within the beam where the sum of the moments of the external loads is not zero.
2. Write the Three Moments Equation: Calculate the distances L1 and L2 from the point of moments to supports 1 and 2. Then, substitute these values and the sum of external moments (M) into the Three Moments Theorem equation.
3. Solve for One Reaction: Rearrange the equation to solve for either R1 or R2, depending on which one is easier to determine.
4. Determine the Other Reaction: Once one reaction is known, substitute it back into the Three Moments equation to solve for the other reaction.
Example:
Consider a continuous beam with two supports A and B, as shown below:
```
A ======[===================================]====== B
P1 = 10 kN P2 = 15 kN q = 5 kN/m, L = 10 m
```
To calculate the reactions at supports A and B, follow these steps:
1. Point of Moments: Choose a point at the middle of the beam, where the support reactions will be equal.
2. Three Moments Equation: The sum of external moments about the middle point is:
```
M = P1 - (L/4) + P2 - (3L/4) + q - (L/2) - (L/4) = 10 kN - (10 m / 4) + 15 kN - (3 - 10 m / 4) + 5 kN/m - (10 m / 2) - (10 m / 4) = 175 kNm
```
3. Solving for R1:
```
0 = R1 - (L/2) - R2 - (L/2) + 175 kNm
```
```
R1 = 175 kN
```
4. Solving for R2:
```
R2 = R1 = 175 kN
```
Therefore, the reactions at supports A and B are both 175 kN.
0