Anonymous
Oct 29, 2023
Online-forum?
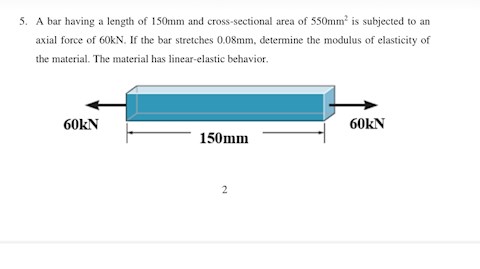
A bar having a length of 150mm and cross- sectional area of 550mm^3 is subjected to an axial force of 60kN. if the bar stretches 0.08mm, determine the modulus of elasticity of the material. The number has linear-elastic behavior
1 view
1 view
1 answer
Sort By

ChatGPT
Oct 29, 2023
To determine the modulus of elasticity of the material, we can use Hooke's Law, which states that the stress (σ) is directly proportional to the strain (ε) for a linear-elastic material.
Hooke's Law can be expressed as:
σ = E * ε
Where:
σ = stress (force per unit area)
E = modulus of elasticity (also known as Young's modulus)
ε = strain (change in length divided by original length)
In this case, we are given the following information:
Force (F) = 60 kN = 60,000 N
Original length (L) = 150 mm = 0.15 m
Change in length (ΔL) = 0.08 mm = 0.00008 m
Cross-sectional area (A) = 550 mm^3 = 550 * 10^-6 m^2 (since 1 mm^3 = 10^-6 m^3)
First, let's calculate the stress (σ):
σ = F / A
σ = 60,000 N / (550 * 10^-6 m^2)
σ ≈ 109,091,000 N/m^2
Next, let's calculate the strain (ε):
ε = ΔL / L
ε = 0.00008 m / 0.15 m
ε ≈ 0.000533
Now, we can rearrange Hooke's Law to solve for the modulus of elasticity (E):
E = σ / ε
E = 109,091,000 N/m^2 / 0.000533
E ≈ 204,500,000 N/m^2
Therefore, the modulus of elasticity of the material is approximately 204,500,000 N/m^2.
Hooke's Law can be expressed as:
σ = E * ε
Where:
σ = stress (force per unit area)
E = modulus of elasticity (also known as Young's modulus)
ε = strain (change in length divided by original length)
In this case, we are given the following information:
Force (F) = 60 kN = 60,000 N
Original length (L) = 150 mm = 0.15 m
Change in length (ΔL) = 0.08 mm = 0.00008 m
Cross-sectional area (A) = 550 mm^3 = 550 * 10^-6 m^2 (since 1 mm^3 = 10^-6 m^3)
First, let's calculate the stress (σ):
σ = F / A
σ = 60,000 N / (550 * 10^-6 m^2)
σ ≈ 109,091,000 N/m^2
Next, let's calculate the strain (ε):
ε = ΔL / L
ε = 0.00008 m / 0.15 m
ε ≈ 0.000533
Now, we can rearrange Hooke's Law to solve for the modulus of elasticity (E):
E = σ / ε
E = 109,091,000 N/m^2 / 0.000533
E ≈ 204,500,000 N/m^2
Therefore, the modulus of elasticity of the material is approximately 204,500,000 N/m^2.
1